Topics
•
Kleene Fixed Point Theorem and Quines (back to Lecture 03)
•
Non-Universal Replication: Langton's Loops
•
The Barricelli Cellular Automaton
•
Wrap-up about Cellular Automata
Wrap-Up about Cellular Automata
•
What are we describing with cellular automata?
•
What should we want for the next scale?
•
What is non-trivial self-replication?
Langton's Loops
Questions about Langton's Loops
•
What is non-trivial replication?
•
Could Langton's loops be blocks of life forms?
•
Is there an analogue of Kleene's theorem here?
Barricelli's (-range) Cellular Automaton
•
Cells are occupied by positive or negative integers, representing their 'velocity'
In one dimension (as was introduced)
•
By default, an integer will 'hop' at every step by its own value (e.g. the number 3 will jump three steps to the right, the number -4 will jump four steps to the right, etc.)
•
Now, when there is a collision (two integers wanting to be at the same location at the next step), the involved integers die
•
Reproduction: if an integer arrives at time at a position which was occupied at time by an integer , then a new integer is put at location , i.e. at a location shifted by the momentum difference
•
Now, the integer we put at location :
•
Can be , simply
•
Or can be a 'hybrid', like a rounded version of the average
This rule was introduced to force numbers to 'cooperate' with other numbers (since we need above)
Why is the Barricelli's system interesting
•
We have an emergence of 'creatures', made of a pattern of numbers, as well as spontaneous reproduction
Emergence
Reproduction
•
There is a diversity that shows up (for some time, at least)
•
There are some phenomena that can be likened to 'parasitism' or 'symbiosis'
While things appear to be rather short-lived (at least in 1D, on fairly small systems), there is definitely something fascinating with Barricelli's system and it is probably somehow under-rated
A possible take-away from Barricelli's work
In some sense, Barricelli made the 'basic' reproduction a trivial problem (emptied it from the solution to the mystery of how it is possible that it emerges), and allows us to worry about 'next scale problems'
It highlights that if some non-trivial interaction between the 'entities' happens, it is fairly easy to see emergence of complexity, which is definitely a desirable feature of life as we would like to capture it
Some interesting alleys for a small project
•
Study the 3D Barricelli automaton, find ways to visualize it and analyze it at large scale
The Barricelli automaton in 2D
•
How does computability theory play a role here?
•
Is Turing-completeness absolutely essential, or is there a weaker notion that works?
•
How far can studying cellular automata bring us towards understanding life in various media?
•
Can the study of continuous systems give us additional insight?



Samples from Barricelli's CA
An attempt to clarify what nontrivial reproduction means and whether Turing-completeness is a necessary condition
A nostalgic video of Langton's CA

A 'data pipe' with no signal
The pictures below come from Langton's paper:

A rightward-traveling signal
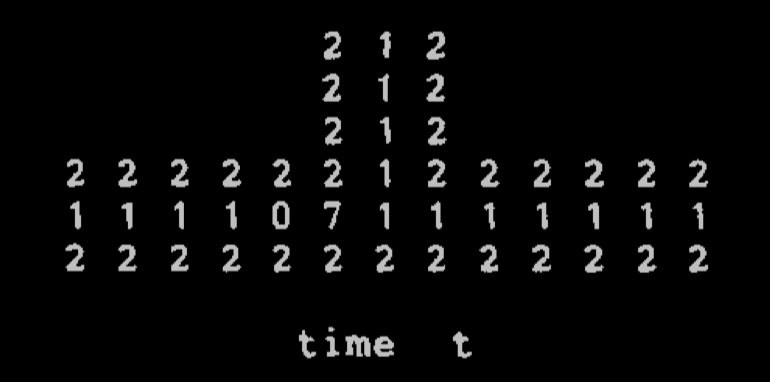
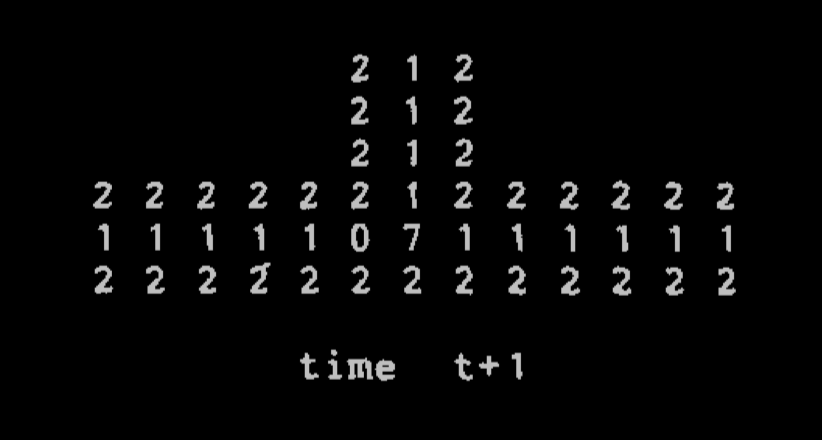
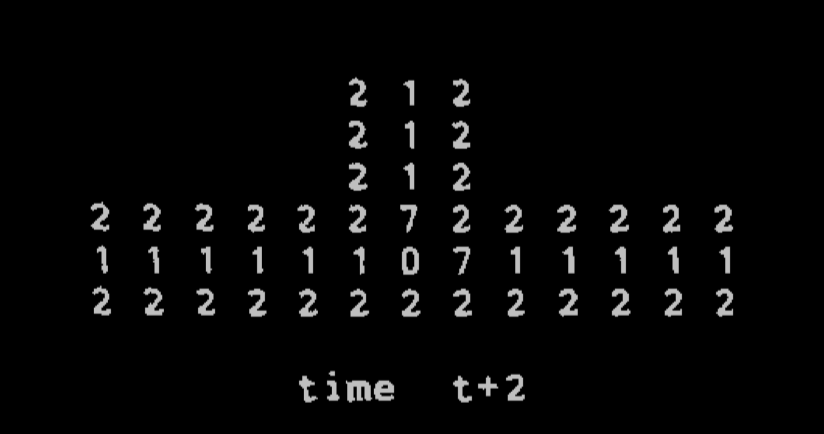
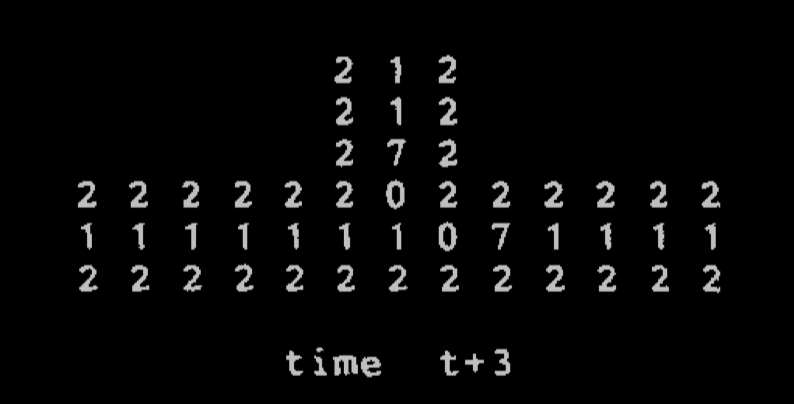
A 'data pipe' junction
Langton took the simplification of Von Neumann's CA done by Codd (an 8-state automaton with simpler 'data pipes'), and made a very simple model of self-replicating loops (which are clearly not Turing-universal, but which he argues display a non-trivial form of self-replication)
One of the key insight in the design is that data is traveling in cycles, and there is no traveling reading head, and we get loops that end up forming a colony of loops
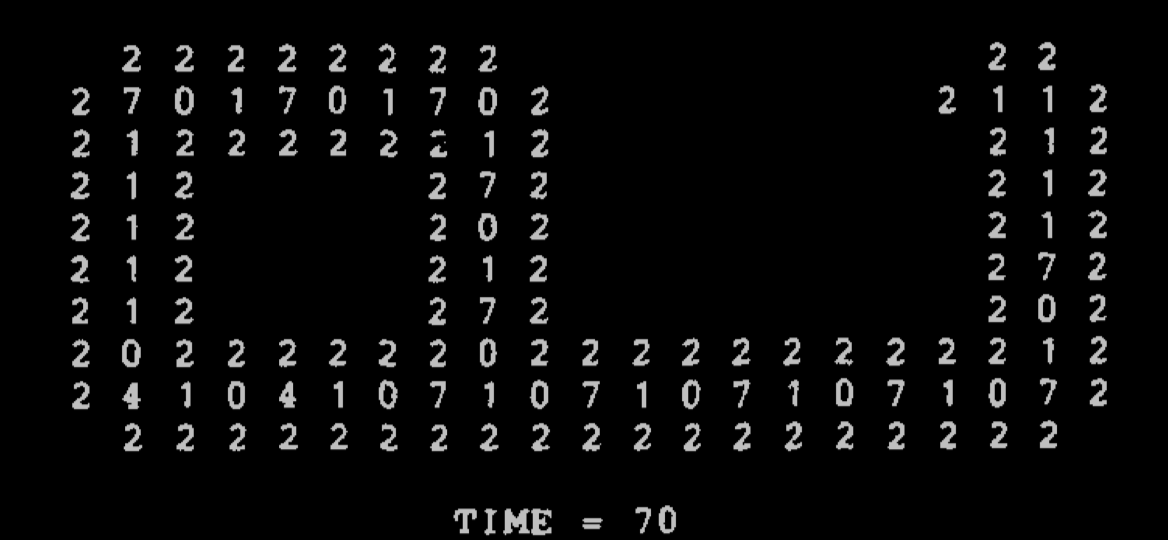
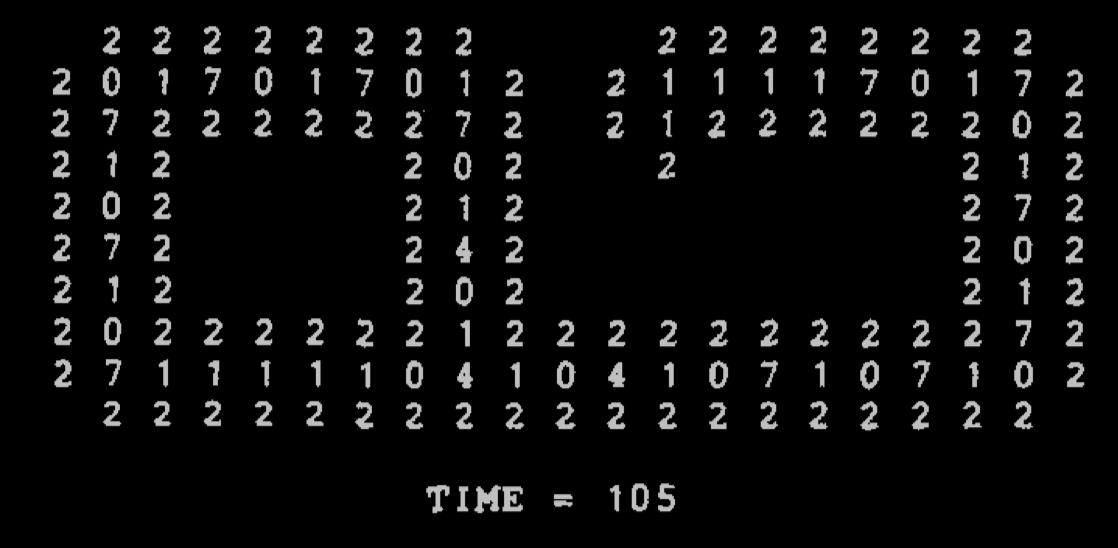
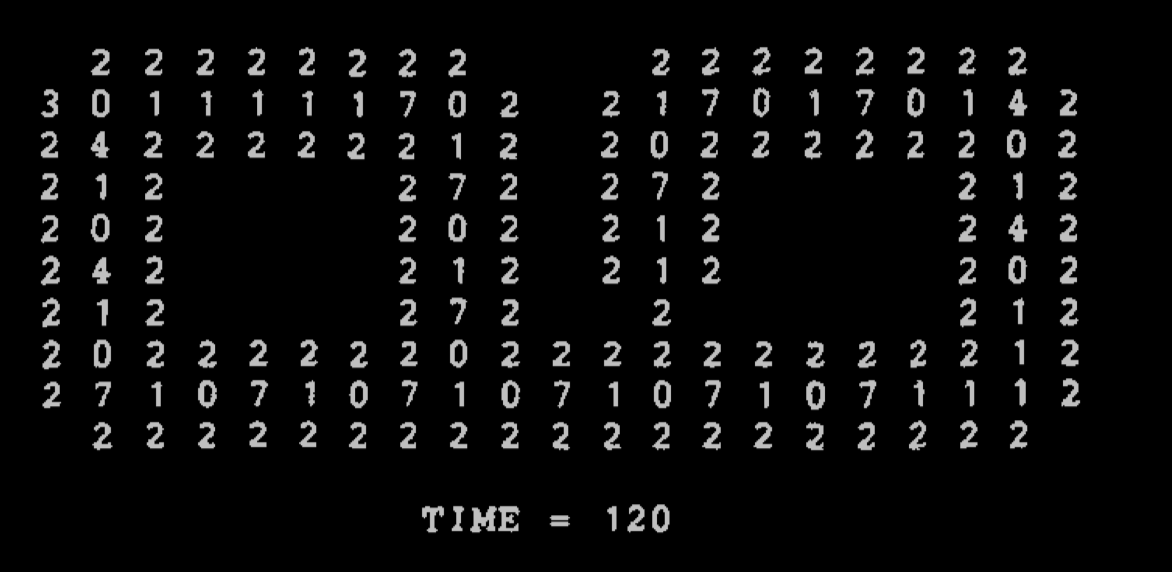
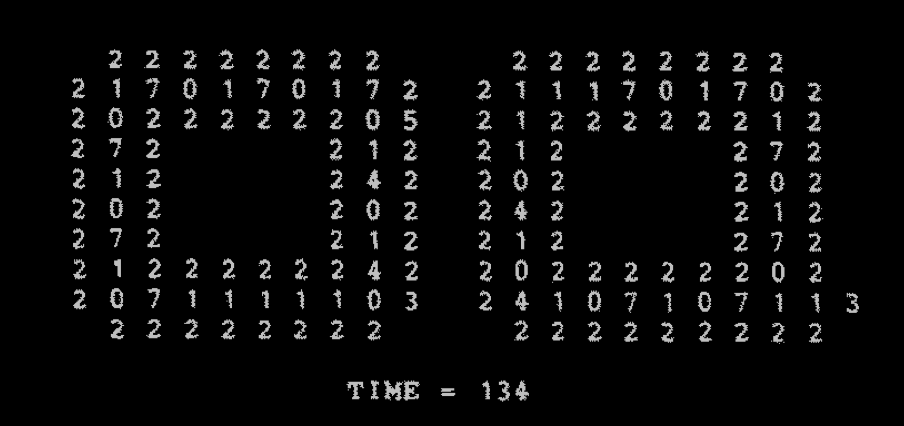
Some steps of the Langton loop's life cycles
•
Do we have a proto-form of Turing-completeness?
•
Maybe strict Turing-completeness is not required: if finite computations of unbounded finite complexity work, is that enough?
•
Can we make modification of the loops so that they are arbitrarily big, store data, and interact with other loops in their colonies?
•
Can we make a theory of open-ended evolution?
•
What do we do about physicality constraints?
We have many questions
What we saw so far
•
Von Neumann's automaton and self-replication
•
The game of life and basic cellular automata questions (Garden of Eden's)
•
Wolfram's proposed classification and emergence
•
Self-replication, life, and irreversibility
•
Can we use arrows of time as measures of life-like processes happening?
.