Quines and the Kleene Fixed-Point Theorem
Quines and the Kleene Fixed-Point Theorem
In the previous lecture, we outlined the general structure of the self-replicator in the Von Neumann 29-state cellular automaton
In the previous lecture, we outlined the general structure of the self-replicator in the Von Neumann 29-state cellular automaton
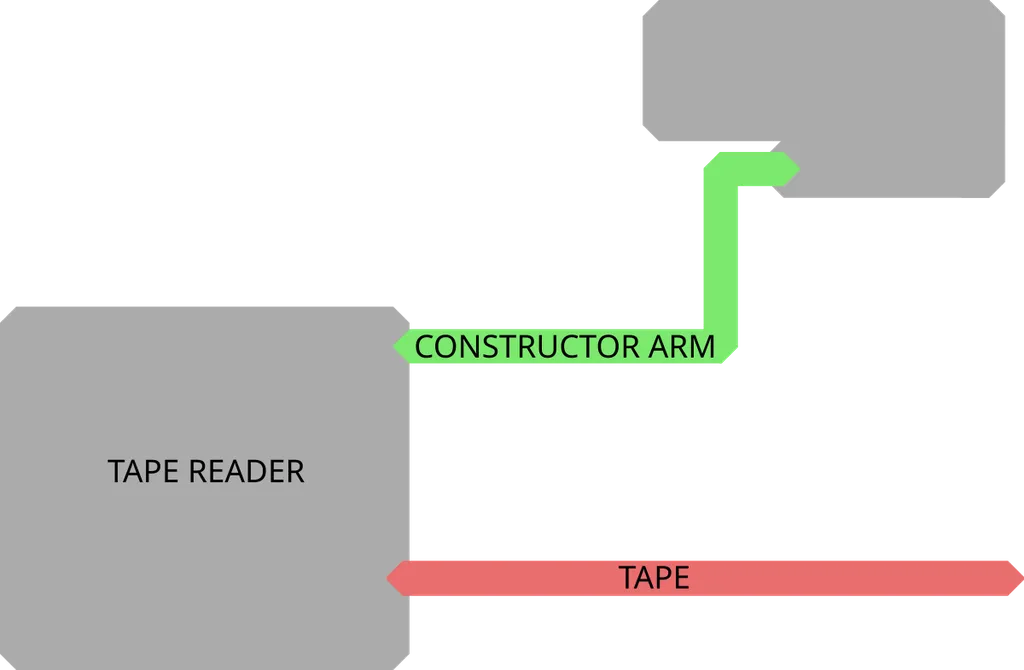
In order for the self-replication process to work, it is enough that _an appropriate (possibly very long) stream of excitations/non-excitations is sent to the construction arm_
In order for the self-replication process to work, it is enough that an appropriate (possibly very long) stream of excitations/non-excitations is sent to the construction arm
So, if our tape reader can somehow read code on the tape, and recognize some instruction like _print_ and read the data that goes after that _print_ and send that data in the form of excitations/non-excitations to the construction arm, we are done
So, if our tape reader can somehow read code on the tape, and recognize some instruction like print and read the data that goes after that print and send that data in the form of excitations/non-excitations to the construction arm, we are done
If we get the right stream, we can definitely make a copy of the tape reader and of the tape itself
If we get the right stream, we can definitely make a copy of the tape reader and of the tape itself
A naive reason why this cannot work
A naive reason why this cannot work
A naive (but wrong) argument why this cannot work: the data needs to explain how to construct the tape reader, the construction arm, _but also the tape itself_... but to describe the tape, we need more tape and so and so forth, so the tape will need to grow, and so we cannot do this with a finite tape
A naive (but wrong) argument why this cannot work: the data needs to explain how to construct the tape reader, the construction arm, but also the tape itself... but to describe the tape, we need more tape and so and so forth, so the tape will need to grow, and so we cannot do this with a finite tape
A vague idea that could work (or not)
A vague idea that could work (or not)
Perhaps, if we could have a compressed version of the tape as an initial condition, we could run a program that decompresses that into a larger version of the data that would correspond to the blueprint of the tape reader, the arm, and the compressed version of the data
Perhaps, if we could have a compressed version of the tape as an initial condition, we could run a program that decompresses that into a larger version of the data that would correspond to the blueprint of the tape reader, the arm, and the compressed version of the data
But what guarantees me I can compress the data?
But what guarantees me I can compress the data?
Obviously, not all data can be compressed, but the magic is that we can do this in this case!
Obviously, not all data can be compressed, but the magic is that we can do this in this case!
A similar (and in fact, identical) problem
A similar (and in fact, identical) problem
The above problem turns out to be essentially identical to that of constructing a quine: a program that outputs its own source code in a programming language
The above problem turns out to be essentially identical to that of constructing a quine: a program that outputs its own source code in a programming language
The program should contain the word "Hello", and is not allowed to access its own source code in the file system (that is "cheating": if we solve the problem this way, it won't help us very much on the original problem)
The program should contain the word "Hello", and is not allowed to access its own source code in the file system (that is "cheating": if we solve the problem this way, it won't help us very much on the original problem)
A naive (failed) attempt in Python
A naive (failed) attempt in Python
For the sake of concreteness, we will focus on python, but the same strategy works in any language
For the sake of concreteness, we will focus on python, but the same strategy works in any language
Ok, now need to print that line
Ok, now need to print that line
But now we need to print that line as well
But now we need to print that line as well
print("print(\"s=\\\"Hello\\\"\")")
But now we need to print that line, and so on and so forth, and we end up with a disaster!
But now we need to print that line, and so on and so forth, and we end up with a disaster!
What would we like to see, anyway?
What would we like to see, anyway?
An idea is that we could want to have a string of characters SOMETHING such that for instance our program that would write its own source code takes the form
An idea is that we could want to have a string of characters SOMETHING such that for instance our program that would write its own source code takes the form
s=process("SOMETHING");print(s)
A good way to formulate the problem
A good way to formulate the problem
We should not so much think that the unknown is "what should we put on the tape" so that when interpreted, the machine builds a copy of itself (though this is certainly what we want)
We should not so much think that the unknown is "what should we put on the tape" so that when interpreted, the machine builds a copy of itself (though this is certainly what we want)
We should think that the tape (initial) state should be of the form
We should think that the tape (initial) state should be of the form
_PRINT(TAPEREADER)/PRINT(ARM)/.../SOMETHING/..._
PRINT(TAPEREADER)/PRINT(ARM)/.../SOMETHING/...
Where SOMETHING is a string (to be found, if it exists) that will ensure that when we run the automaton, a copy of the whole thing, including the SOMETHING (of course, and this is the tricky point)
Where SOMETHING is a string (to be found, if it exists) that will ensure that when we run the automaton, a copy of the whole thing, including the SOMETHING (of course, and this is the tricky point)
So this is exactly of the same formulation as the Von Neumann situation with
So this is exactly of the same formulation as the Von Neumann situation with
A successful implementation
A successful implementation
_PRINT(TAPEREADER)/PRINT(ARM)/.../SOMETHING/..._
PRINT(TAPEREADER)/PRINT(ARM)/.../SOMETHING/...
In some sense, we want to define a wrapping function:
In some sense, we want to define a wrapping function:
def wrap(stuff):
return 's=process("' + stuff + '");print(s)'
And we would like to find a SOMETHING string, such that
And we would like to find a SOMETHING string, such that
process(SOMETHING)==wrap(SOMETHING)
So, if we write this into an abstract language, it means that we have a function $h:string->string$ (the function wrap here) and we are looking for something such that $evaluation(h(stuff))=evaluation(stuff)$
So, if we write this into an abstract language, it means that we have a function
h:string−>string (the function wrap here) and we are looking for something such that
evaluation(h(stuff))=evaluation(stuff)So, this is to say that stuff is a fixed point of $h$ _when viewed through the angle of the evaluation_ (this is not to say that $h$ must have a fixed point per se)
So, this is to say that stuff is a fixed point of
h when viewed through the angle of the evaluation (this is not to say that
h must have a fixed point per se)
So, how can we prove that this string exists?
So, how can we prove that this string exists?
The idea is that this string is a kind of cool paradoxical string, which is the result of taking a certain wrapautofeed function (which eats strings and returns strings), and applying that wrapautofeed function to its own source code (so, we will get a bona fide string)
The idea is that this string is a kind of cool paradoxical string, which is the result of taking a certain wrapautofeed function (which eats strings and returns strings), and applying that wrapautofeed function to its own source code (so, we will get a bona fide string)
So, what is the wrapautofeed function? It is the function that takes a string and evaluates it as a program on itself, and then wraps the result (we call this 'waf' for 'wrapautofeed')
So, what is the wrapautofeed function? It is the function that takes a string and evaluates it as a program on itself, and then wraps the result (we call this 'waf' for 'wrapautofeed')
def waf(string): return wrap(process(string)(string))
So, we can now define $wafcode$ as the string of the code of waf:
So, we can now define
wafcode as the string of the code of waf:
wafcode='def waf(string): return wrap(process(string)(string))'
And our fixed point is then
And our fixed point is then
So... why is $prequine$ such that $wrap(prequine)==process(prequine)$ ?
So... why is
prequine such that
wrap(prequine)==process(prequine) ?
The idea is that $wrap(prequine)=wrap(waf(wafcode))$ and now that this is by definition $waf(wafcode)$ which is $prequine$
The idea is that
wrap(prequine)=wrap(waf(wafcode)) and now that this is by definition
waf(wafcode) which is
prequineKleene Fixed-Point Theorem
Kleene Fixed-Point Theorem
The Kleene fixed point theorem is an abstract way in which this can be done:
The Kleene fixed point theorem is an abstract way in which this can be done:
To be seen in a demo
To be seen in a demo
Data-vs-code idea
•
Data-vs-code idea
Doing something seemingly impossible
•
Doing something seemingly impossible
Solving the quine problem is essentially the same as solving the self-replication problem, if we have a Turing machine structure
•
Solving the quine problem is essentially the same as solving the self-replication problem, if we have a Turing machine structure
This is essentially what happens in DNA
•
This is essentially what happens in DNA
Here process(string) evaluates the string as a python code, and applies the result of that evaluation to the string (viewed as a string)
Here process(string) evaluates the string as a python code, and applies the result of that evaluation to the string (viewed as a string)
The Y-Combinator
The Y-Combinator
$Y=\lambda f.(\lambda x.f(x \, x)) (\lambda x.f(x \, x))$
Y=λf.(λx.f(xx))(λx.f(xx)) A super concise way to summarize the quine constructions
A super concise way to summarize the quine constructions
In our language Y-combinator transforms a wrapper function (that is language-dependent) into a prequine for that language (i.e. something that when processed or wrapped will give the same thing)
In our language Y-combinator transforms a wrapper function (that is language-dependent) into a prequine for that language (i.e. something that when processed or wrapped will give the same thing)
The conceptual idea is that if we one-step evaluate $Yf$ (by thinking "Ok, so we want to take the first parenthesis, which says feed your argument to itself and wrap by $f$"), we get $Yf=f(p2\,p2)$, where $p2$ is the second parenthesis
The conceptual idea is that if we one-step evaluate
Yf (by thinking "Ok, so we want to take the first parenthesis, which says feed your argument to itself and wrap by
f"), we get
Yf=f(p2p2), where
p2 is the second parenthesis
Beware of the Infinite Evaluation
Beware of the Infinite Evaluation
If we try to evaluate naively ('deeply' would be naive here) the Y-combinator, we get a kind a kind of infinite loop:
If we try to evaluate naively ('deeply' would be naive here) the Y-combinator, we get a kind a kind of infinite loop:
Since the second argument $p2$ is in fact still $(\lambda x. f(x\,x))$, we get that $Yf=f(p2\,p2)=f((\lambda x.f(x \,x)(\lambda x\,f(x\,x))=f(Yf)$
Since the second argument
p2 is in fact still
(λx.f(xx)), we get that
Yf=f(p2p2)=f((λx.f(xx)(λxf(xx))=f(Yf)Note that intuitively this is what we could want, since an infinite number of applications of $f$ is something that indeed should be a fixed point of applying the wrapper $f$... but the point is that the expression should be understood as code that _can be evaluated_ but _does not need_ to be evaluated all the time
Note that intuitively this is what we could want, since an infinite number of applications of
f is something that indeed should be a fixed point of applying the wrapper
f... but the point is that the expression should be understood as code that
can be evaluated but
does not need to be evaluated all the time
This is a bit similar to the idea: if we have a quine, we can execute it and it will print its source code again, and so if we were to re-execute that code, it would yield something that would loop infinitely; but in itself, a quine is not something that loops infinitely (of course the point of reproduction is that it should not particularly stop at a specific location)
This is a bit similar to the idea: if we have a quine, we can execute it and it will print its source code again, and so if we were to re-execute that code, it would yield something that would loop infinitely; but in itself, a quine is not something that loops infinitely (of course the point of reproduction is that it should not particularly stop at a specific location)
Deferred Evaluation
Deferred Evaluation
Formally, the Y-combinator construction is a 'deferred' evaluation construction of the loop that would repeat the evaluation of $f$ onto the variable $x$ infinitely-many times
Formally, the Y-combinator construction is a 'deferred' evaluation construction of the loop that would repeat the evaluation of
f onto the variable
x infinitely-many times
One step in, we get $\lambda x.(f(\lambda x.f(x\,x)\, \lambda x.f(x\,x)))$, which is $f(Yf)$, but if we keep evaluating, we get $f(f(Yf))$, and if we keep evaluating $Yf$, we get $f(f(f(Yf)))$, and so on and so forth
One step in, we get
λx.(f(λx.f(xx)λx.f(xx))), which is
f(Yf), but if we keep evaluating, we get
f(f(Yf)), and if we keep evaluating
Yf, we get
f(f(f(Yf))), and so on and so forth
The idea is that the fixed point should not be the evaluation itself (it returns no value), but the code suggesting the evaluation is a fixed point (no one forces you to evaluate the code! it is a perfectly valid string)
The idea is that the fixed point should not be the evaluation itself (it returns no value), but the code suggesting the evaluation is a fixed point (no one forces you to evaluate the code! it is a perfectly valid string)
It is a bit like saying that we should study an animal for what it is, not for the possible consequences of its descendents on the universe (which would be much harder)
It is a bit like saying that we should study an animal for what it is, not for the possible consequences of its descendents on the universe (which would be much harder)
It can mean several thing, but in the case of Python programs or of Turing-tape programs, it is enough that the 'process' or 'evaluate' function replaces a specific string (say '\$', aka chr(36)) in python by the argument given to it
It can mean several thing, but in the case of Python programs or of Turing-tape programs, it is enough that the 'process' or 'evaluate' function replaces a specific string (say '$', aka chr(36)) in python by the argument given to it
Kleene Fixed Point Theorem and Quines
Kleene Fixed Point Theorem and Quines
First, it is helpful to find quines following the proof of the fixed point theorem
First, it is helpful to find quines following the proof of the fixed point theorem
Maybe something of the following form:
Maybe something of the following form:
Using the Kleene fixed point argume, we can definitely solve this problem
Using the Kleene fixed point argume, we can definitely solve this problem
Following this, an 'almost solution' (just with a few wrong quotemarks) is
Following this, an 'almost solution' (just with a few wrong quotemarks) is
s=eval("(lambda s: s.replace(chr(36), s))('s=eval((lambda s: s.replace(chr(36), s))($));print(s)')");print(s)
Note how the 'autofeed' code is
Note how the 'autofeed' code is
lambda s: s.replace(chr(36), s)
Which just replaces an instance of the dollar sign (which we represent with _chr(36)_ rather than a _\$_) with _s_: this way _s_ can be both code (something that contains dollars to be replaced) and data a pure string
Which just replaces an instance of the dollar sign (which we represent with chr(36) rather than a $) with s: this way s can be both code (something that contains dollars to be replaced) and data a pure string
A 'full' (much less pretty) solution fixing the quotemark issues could be for instance:
A 'full' (much less pretty) solution fixing the quotemark issues could be for instance:
s=eval("(lambda s: s.replace(chr(36), s.replace(chr(34), chr(92)+chr(34))).replace(chr(41)+chr(40)+chr(115),chr(41)+chr(40)+chr(39)+chr(115)).replace(chr(115)+chr(41)+chr(41), chr(115)+chr(41)+chr(39)+chr(41)))('s=eval(\"(lambda s: s.replace(chr(36), s.replace(chr(34), chr(92)+chr(34))).replace(chr(41)+chr(40)+chr(115),chr(41)+chr(40)+chr(39)+chr(115)).replace(chr(115)+chr(41)+chr(41), chr(115)+chr(41)+chr(39)+chr(41)))($)\");print(s)')");print(s)
About What the Process Means
About What the Process Means
So, when we evaluate the above expression, we are really evaluating autofeed of wrap-autofeed-code, which is wrap-auto-feed of wrap-auto-feed-code, which is wrap of the expression, as desired
So, when we evaluate the above expression, we are really evaluating autofeed of wrap-autofeed-code, which is wrap-auto-feed of wrap-auto-feed-code, which is wrap of the expression, as desired
.