Von Neumann Cellular Automaton & Replicator

Von Neumann Cellular Automaton & Replicator

Description of Von Neumann's 29-State CA

Description of Von Neumann's 29-State CA

Self-Replicator: Low-Level Building Blocks

Self-Replicator: Low-Level Building Blocks

In the late 1940s, Von Neumann wrote the 'Theory of Self-Reproducing Cellular Automata', an unfinished 400-page manuscript describing what would be called the _logical basis of self-reproduction_

In the late 1940s, Von Neumann wrote the 'Theory of Self-Reproducing Cellular Automata', an unfinished 400-page manuscript describing what would be called the logical basis of self-reproduction

This manuscript describes a 29-state cellular automaton, together with a sketch for a universal self-replicating machine in it, detailing the many elements needed for its construction

This manuscript describes a 29-state cellular automaton, together with a sketch for a universal self-replicating machine in it, detailing the many elements needed for its construction

This construction is very remarkable for many aspects:

This construction is very remarkable for many aspects:

The invention of cellular automata as a framework where the principles of self-reproduction could be clearly outlined

•

The invention of cellular automata as a framework where the principles of self-reproduction could be clearly outlined

The idea of building a Turing machine inside of it (this would later be called 'Turing-completeness' of the automaton)

•

The idea of building a Turing machine inside of it (this would later be called 'Turing-completeness' of the automaton)

The leveraging of Turing completeness as a means to reveal how self-reproduction follows

•

The leveraging of Turing completeness as a means to reveal how self-reproduction follows

The incredible cleverness of the construction, and the grit needed to go through it

•

The incredible cleverness of the construction, and the grit needed to go through it

Some clever remarks about reversibility, open-ended evolution, etc. that we can argue were not understood very well by later generations

•

Some clever remarks about reversibility, open-ended evolution, etc. that we can argue were not understood very well by later generations

What is the problem that was solved?

What is the problem that was solved?

The construction of Von Neumann may perhaps look a bit unusual, in that it is a very involved mathematical construction that does not necessarily appear to be a proof of an a priori well-posed mathematical statement

The construction of Von Neumann may perhaps look a bit unusual, in that it is a very involved mathematical construction that does not necessarily appear to be a proof of an a priori well-posed mathematical statement

In the research world it is in fact not that unusual to first _discover something nontrivial_ and then find out _what we just proved using it_

In the research world it is in fact not that unusual to first discover something nontrivial and then find out what we just proved using it

This is however a bit of a special case in that it _appears quite challenging to find one statement that this is a proof of_, and that it also could _conceivably be interpreted as a proof of several fairly different statements_

This is however a bit of a special case in that it appears quite challenging to find one statement that this is a proof of, and that it also could conceivably be interpreted as a proof of several fairly different statements

The reason is that Von Neumann invented one cellular automaton and then solved the (very difficult) problem of self-replication in that cellular automaton...

The reason is that Von Neumann invented one cellular automaton and then solved the (very difficult) problem of self-replication in that cellular automaton...

And yet we could ask the question: would there not be a simpler set of rules where self-replication can just occur (in a naive sense at least)

And yet we could ask the question: would there not be a simpler set of rules where self-replication can just occur (in a naive sense at least)

So, we could of course say that Von Neumann's construction strength is that it solves the problem in a difficult setup, but there are _many ways in which things can be made difficult_, so some naturality should be argued here

So, we could of course say that Von Neumann's construction strength is that it solves the problem in a difficult setup, but there are many ways in which things can be made difficult, so some naturality should be argued here

Another route would be to say that we want some construction where we have a universal self-replicator that can do any computation, but then that makes the idea of putting a Turing machine an obvious one, and it is definitely a post-hoc statement, so that is not goo either

Another route would be to say that we want some construction where we have a universal self-replicator that can do any computation, but then that makes the idea of putting a Turing machine an obvious one, and it is definitely a post-hoc statement, so that is not goo either

The most honest simple answer is that the solution that Von Neumann constructed for the problem of self-replication in his 29-state automaton is in some sense universal with respect to rules: with roughly the same strategy, one can construct a self-replicator in the game of life, and it appears to be a solution similar to the one that life as we know it solved our universe for instance

The most honest simple answer is that the solution that Von Neumann constructed for the problem of self-replication in his 29-state automaton is in some sense universal with respect to rules: with roughly the same strategy, one can construct a self-replicator in the game of life, and it appears to be a solution similar to the one that life as we know it solved our universe for instance

Of course, that is not very well posed mathematically as a statement... could we find a statement that we will actually prove?

Of course, that is not very well posed mathematically as a statement... could we find a statement that we will actually prove?

In some sense, what makes self-reproduction a remarkable phenomenon is in no small part due to the fact that it is a phenomenon that does not happen e.g. on the Moon (for now, at least)

In some sense, what makes self-reproduction a remarkable phenomenon is in no small part due to the fact that it is a phenomenon that does not happen e.g. on the Moon (for now, at least)

So, a good mathematical problem is: exhibit self-reproduction in an environment where it appears to be _against the odds_, e.g. where there can be no self-replicators of small sizes

So, a good mathematical problem is: exhibit self-reproduction in an environment where it appears to be against the odds, e.g. where there can be no self-replicators of small sizes

If we look at Von Neumann's cellular automaton, with its 29 states, the fact that only the four immediate neighbors can influence, and the corresponding rules (which have a lot of symmetries), the amount of information we feed into its description is not huge

If we look at Von Neumann's cellular automaton, with its 29 states, the fact that only the four immediate neighbors can influence, and the corresponding rules (which have a lot of symmetries), the amount of information we feed into its description is not huge

And now, if we ask if there are self-replicators of size 100, the answer is (almost certainly) no, if there are some of size 200, the answer is no again, of size 1000, the answer is no again, ..., of size 10000, the answer is (probably) no, and if we go to size 200000 (and any number above it), the answer is _yes_, and this is remarkable

And now, if we ask if there are self-replicators of size 100, the answer is (almost certainly) no, if there are some of size 200, the answer is no again, of size 1000, the answer is no again, ..., of size 10000, the answer is (probably) no, and if we go to size 200000 (and any number above it), the answer is yes, and this is remarkable

Technically, there could be some isolated self-replicator points for some specific sizes in a cellular automaton, but it is typically not a phenomenon that we seem to see if we look at the answers to the question for various sizes, and yet, once we pass a threshold the answer becomes invariably yes

Technically, there could be some isolated self-replicator points for some specific sizes in a cellular automaton, but it is typically not a phenomenon that we seem to see if we look at the answers to the question for various sizes, and yet, once we pass a threshold the answer becomes invariably yes

The other part of the answer goes beyond the question of self-reproduction (we can expect the construction to be usable to display intelligence, evolution, etc.), but that is even less of the form of 'what is the nontrivial question that we solved'

The other part of the answer goes beyond the question of self-reproduction (we can expect the construction to be usable to display intelligence, evolution, etc.), but that is even less of the form of 'what is the nontrivial question that we solved'

A first design element: quiescent states

A first design element: quiescent states

It is important that any construction only relies on a finite amount of information, and preferably in a local way, so there should be a quiescent state that occupies all but a finite number of sites of the grid

It is important that any construction only relies on a finite amount of information, and preferably in a local way, so there should be a quiescent state that occupies all but a finite number of sites of the grid

This is of course mathematically more elegant, but it also has natural practical motivations

This is of course mathematically more elegant, but it also has natural practical motivations

A second design element: circuits & excitations

A second design element: circuits & excitations

The central idea of the construction is to allow for the processing of information, which in particular involves _carrying_ information across the grid

The central idea of the construction is to allow for the processing of information, which in particular involves carrying information across the grid

This leads to the idea of have certain states come in two versions: excited '1' or not excited '0'

This leads to the idea of have certain states come in two versions: excited '1' or not excited '0'

So, we have 28 states left for our description

So, we have 28 states left for our description

To know where the excitations move, we need a direction also, so this gives four directions

To know where the excitations move, we need a direction also, so this gives four directions

The idea in the construction is that unexcited configurations should just stay stable, and could be sparked with excitations... this is fairly close to the way that computers work

The idea in the construction is that unexcited configurations should just stay stable, and could be sparked with excitations... this is fairly close to the way that computers work

So, at this point, we have eight ($4\times2$) 'wire' states that carry informational content... but we need information processing... we draw them inblue, with a yellow dot to represent excited versions:

So, at this point, we have eight ($4\times2$) 'wire' states that carry informational content... but we need information processing... we draw them inblue, with a yellow dot to represent excited versions:

Third Design Element: Information Processing

Third Design Element: Information Processing

In order to process information, it is enough to be able to perform a 'split', a 'not', and an 'and', and to have a way to time things (we will need a 'clock' for our machine)

In order to process information, it is enough to be able to perform a 'split', a 'not', and an 'and', and to have a way to time things (we will need a 'clock' for our machine)

The way this is done by Von Neumann's construction is somehow non-standard: he introduces eight more 'wire' states, which are called the _special_ directional elements, and which we represent in red (by opposition to the _ordinary_ elements, which we represent in blue)

The way this is done by Von Neumann's construction is somehow non-standard: he introduces eight more 'wire' states, which are called the special directional elements, and which we represent in red (by opposition to the ordinary elements, which we represent in blue)

Excitations don't propagate from ordinary to special or vice versa: in fact if an excitation of a special states arrives to an ordinary state, that ordinary state is 'killed' (it becomes quiescent); similarly if an ordinary excitation arrives to a special state, that special state is killed as well

Excitations don't propagate from ordinary to special or vice versa: in fact if an excitation of a special states arrives to an ordinary state, that ordinary state is 'killed' (it becomes quiescent); similarly if an ordinary excitation arrives to a special state, that special state is killed as well

A simple way to remember this is to think in a Cold War analogy: the ordinary states represent the Allies, while the special states represent the Soviets (that is the reason why we chose to draw them in blue/red)

A simple way to remember this is to think in a Cold War analogy: the ordinary states represent the Allies, while the special states represent the Soviets (that is the reason why we chose to draw them in blue/red)

So, we have now 1 quiescent, 8 ordinary and 8 special states...

So, we have now 1 quiescent, 8 ordinary and 8 special states...

An important idea is that we will be able to move the wires (both ordinary and special) by destroying them (and creating them elsewhere, but that needs to be explained)

An important idea is that we will be able to move the wires (both ordinary and special) by destroying them (and creating them elsewhere, but that needs to be explained)

The last important design element is the so-called 'confluent' state; it acts both an AND and as a delay, and as a bridge from ordinary to special excitations

The last important design element is the so-called 'confluent' state; it acts both an AND and as a delay, and as a bridge from ordinary to special excitations

The confluent state has two bits of information in storage, so it counts as four states

The confluent state has two bits of information in storage, so it counts as four states

We can say it has an 'in' bit and an 'out' bit

We can say it has an 'in' bit and an 'out' bit

The 'in' bit is the AND of the incoming ordinary states: at time $t+1$, the 'in' bit is '1' if and only if all the adjcent incoming ordinary states at time $t$ are excited

The 'in' bit is the AND of the incoming ordinary states: at time $t+1$, the 'in' bit is '1' if and only if all the adjcent incoming ordinary states at time $t$ are excited

If a special excitation arrives to a confluent state it dies, so the only excitations the confluent will accept are ordinary ones

If a special excitation arrives to a confluent state it dies, so the only excitations the confluent will accept are ordinary ones

The 'out' bit is just the 'in' state of the previous step

The 'out' bit is just the 'in' state of the previous step

The Von Neumann CA is a discrete-time nearest neighbor automaton: for each $t\in\mathbb N$, the state at point $(x,y)$ at time $t+1%$ is a function of the states at $(x,y),(x\pm1,y),(x,y\pm1)$ at time $t$

The Von Neumann CA is a discrete-time nearest neighbor automaton: for each $t\in\mathbb N$, the state at point $(x,y)$ at time $t+1$ is a function of the states at $(x,y),(x\pm1,y),(x,y\pm1)$ at time $t$

All the 'non-incoming' 'wire' state (both ordinary and special) adjacent to a confluent state are excited by its 'out' state: if an adjacent confluent state has 'out' bit equal to $1$ at time $t$, then all wire states that don't point to it will be $1$ at time $t+1$

All the 'non-incoming' 'wire' state (both ordinary and special) adjacent to a confluent state are excited by its 'out' state: if an adjacent confluent state has 'out' bit equal to $1$ at time $t$, then all wire states that don't point to it will be $1$ at time $t+1$

So, each of these ordinary states acts as an 'OR' of the excitations that come to it in the various directions

So, each of these ordinary states acts as an 'OR' of the excitations that come to it in the various directions

So... we are almost done for the description of the automaton's rule...

So... we are almost done for the description of the automaton's rule...

We just need a way to 'edit' the world, i.e. transform a quiescent state into an ordinary or special or confluent one (we already have ways to transform any non-quiescent state into a quiescent one if we send an excitation of the correct type)

We just need a way to 'edit' the world, i.e. transform a quiescent state into an ordinary or special or confluent one (we already have ways to transform any non-quiescent state into a quiescent one if we send an excitation of the correct type)

The idea is simply that we will inject, using 'wire' states a specific sequence of excitations/non-excitations: as soon as a 'wire' state points to a quiescent state, it becomes 'sensitized' and it starts 'listening' for the next steps, and it will become one of the 9 unexcited wire or confluent states

The idea is simply that we will inject, using 'wire' states a specific sequence of excitations/non-excitations: as soon as a 'wire' state points to a quiescent state, it becomes 'sensitized' and it starts 'listening' for the next steps, and it will become one of the 9 unexcited wire or confluent states

So, this gives us the eight sensitized states (containing the values that we may end up seeing)

So, this gives us the eight sensitized states (containing the values that we may end up seeing)

Loop

Loop

Clocks

Clocks

Pulsar

Pulsar

Switch

Switch

Tape Reader

Tape Reader

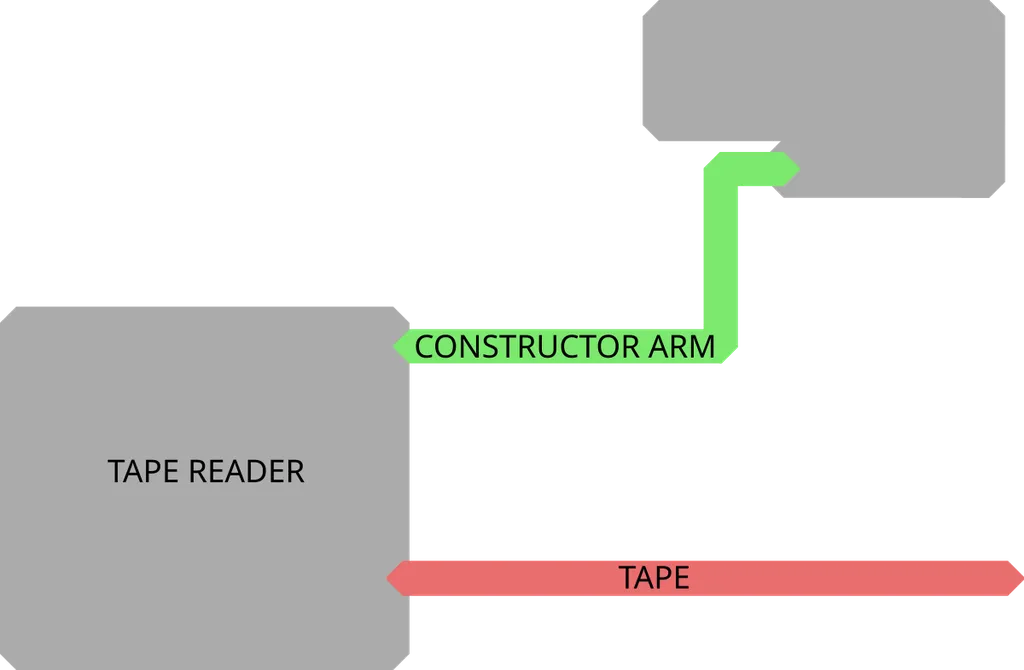
Arm Extension

Arm Extension

Advanced Tape

Advanced Tape

Confluent State

Confluent State

It has two bits of information: an 'in' and an 'out' bit, so this is 4 states

It has two bits of information: an 'in' and an 'out' bit, so this is 4 states

The 'in' bit takes the AND of the excitations of the incoming ordinary (blue) 'wire' states at the previous step

The 'in' bit takes the AND of the excitations of the incoming ordinary (blue) 'wire' states at the previous step

The 'out' bit takes the value of the 'in' bit at the previous step

The 'out' bit takes the value of the 'in' bit at the previous step

The 'out' bit excites the non-incoming both ordinary and special 'wire' states at the next step

The 'out' bit excites the non-incoming both ordinary and special 'wire' states at the next step

The confluent doesn't like special very much: if it receives an incoming special excitation, it becomes quiescent

The confluent doesn't like special very much: if it receives an incoming special excitation, it becomes quiescent

The confluent does not directly influence (and is not directly influenced by) the other confluent states

The confluent does not directly influence (and is not directly influenced by) the other confluent states

How the the machine works in the end

How the the machine works in the end

It is enough to send the correct string of excitations through the construction arm

It is enough to send the correct string of excitations through the construction arm

And these excitations can be commanded by a computer

And these excitations can be commanded by a computer

The apparent paradox is that it is a lot of information to use, because whenever we use cells to describe the information to describe the machine, but if we naively just add information for that on a tape, that information will need to be further copied

The apparent paradox is that it is a lot of information to use, because whenever we use cells to describe the information to describe the machine, but if we naively just add information for that on a tape, that information will need to be further copied

So, naively, we would not be able to make a copy of the whole thing

So, naively, we would not be able to make a copy of the whole thing

But that's wrong: because of the power of self-reference, we can make the data copy itself

But that's wrong: because of the power of self-reference, we can make the data copy itself

Decoder

Decoder

The full tape reader (without the tape)

The full tape reader (without the tape)

Sketch of How Things will work

Sketch of How Things will work

We just need to write the right program so that the correct stream of excitations/non-excitations goes through the system and constructs a copy of the tape reader, the construction arm, and of the tape

We just need to write the right program so that the correct stream of excitations/non-excitations goes through the system and constructs a copy of the tape reader, the construction arm, and of the tape