Classification of Cellular Automata
Classification of Cellular Automata
In the previous lectures, we have outlined a number of interesting features or behaviors for cellular automata (self-replication, Turing-completeness, Gardens of Eden, reversibility), and for each of these, we exhibited examples of rules and of relevant configurations for these rules
In the previous lectures, we have outlined a number of interesting features or behaviors for cellular automata (self-replication, Turing-completeness, Gardens of Eden, reversibility), and for each of these, we exhibited examples of rules and of relevant configurations for these rules
Today we discuss the somehow symmetric question: if we take a 'random' (or 'typical', if you prefer) cellular automaton, and we take a random configuration
Today we discuss the somehow symmetric question: if we take a 'random' (or 'typical', if you prefer) cellular automaton, and we take a random configuration
The study of these questions was spearheaded by Stephen Wolfram, who extensively studied the one-dimensional cellular automata (particularly nearest-neighbor 2-state ones) and proposed a classification of cellular automata into four classes
The study of these questions was spearheaded by Stephen Wolfram, who extensively studied the one-dimensional cellular automata (particularly nearest-neighbor 2-state ones) and proposed a classification of cellular automata into four classes
Nearest-Neighbor 1D 2-State Cellular Automata
Nearest-Neighbor 1D 2-State Cellular Automata
A priori, since the number of relevant configurations for a nearest-neighbor automaton 2-state is $2^3=8$ (the cell and its two neighbors) and so there are $2^8=256$ possible rules
A priori, since the number of relevant configurations for a nearest-neighbor automaton 2-state is
23=8 (the cell and its two neighbors) and so there are
28=256 possible rules
There is a standard notation for these rules, which consists in giving them numbers between $0$ and $255$ which was invented by Wolfram
There is a standard notation for these rules, which consists in giving them numbers between
0 and
255 which was invented by Wolfram
Then the field drifted away from alife
Then the field drifted away from alife
How to study a 'random' cellular automaton?
•
How to study a 'random' cellular automaton?
The Wolfram's four classes
•
The Wolfram's four classes
The undecidability questions
•
The undecidability questions
The Halting Problem via diagonalization
•
The Halting Problem via diagonalization
The class IV cellular automata
•
The class IV cellular automata
What does it mean to be 'Turing complete'?
•
What does it mean to be 'Turing complete'?
Can the classification be made sense of?
•
Can the classification be made sense of?
What is interesting about rule 110?
•
What is interesting about rule 110?
Langton's $\lambda$ function
•
Langton's
λ function
If we write the numbers $0,1,\ldots,7$ in binary (as $000, 001, ..., 111$), they correspond to $3$ adjacent bits, and if we write the bit 'next-value' that they yield for the central bit we obtain an $8$-bit number. If we read it from _right to left_ that can be viewed as a number between $0$ and $255$
If we write the numbers
0,1,…,7 in binary (as
000,001,...,111), they correspond to
3 adjacent bits, and if we write the bit 'next-value' that they yield for the central bit we obtain an
8-bit number. If we read it from
right to left that can be viewed as a number between
0 and
255If we want $0$ to represent a 'quiescent' state, $000$ needs to get mapped to $0$, and thus leading to an even number
If we want
0 to represent a 'quiescent' state,
000 needs to get mapped to
0, and thus leading to an even number
A Small Gallery of Rules
A Small Gallery of Rules
(With a single seed and/or with random initial configurations)
(With a single seed and/or with random initial configurations)
Wolfram's Proposed Classification
Wolfram's Proposed Classification
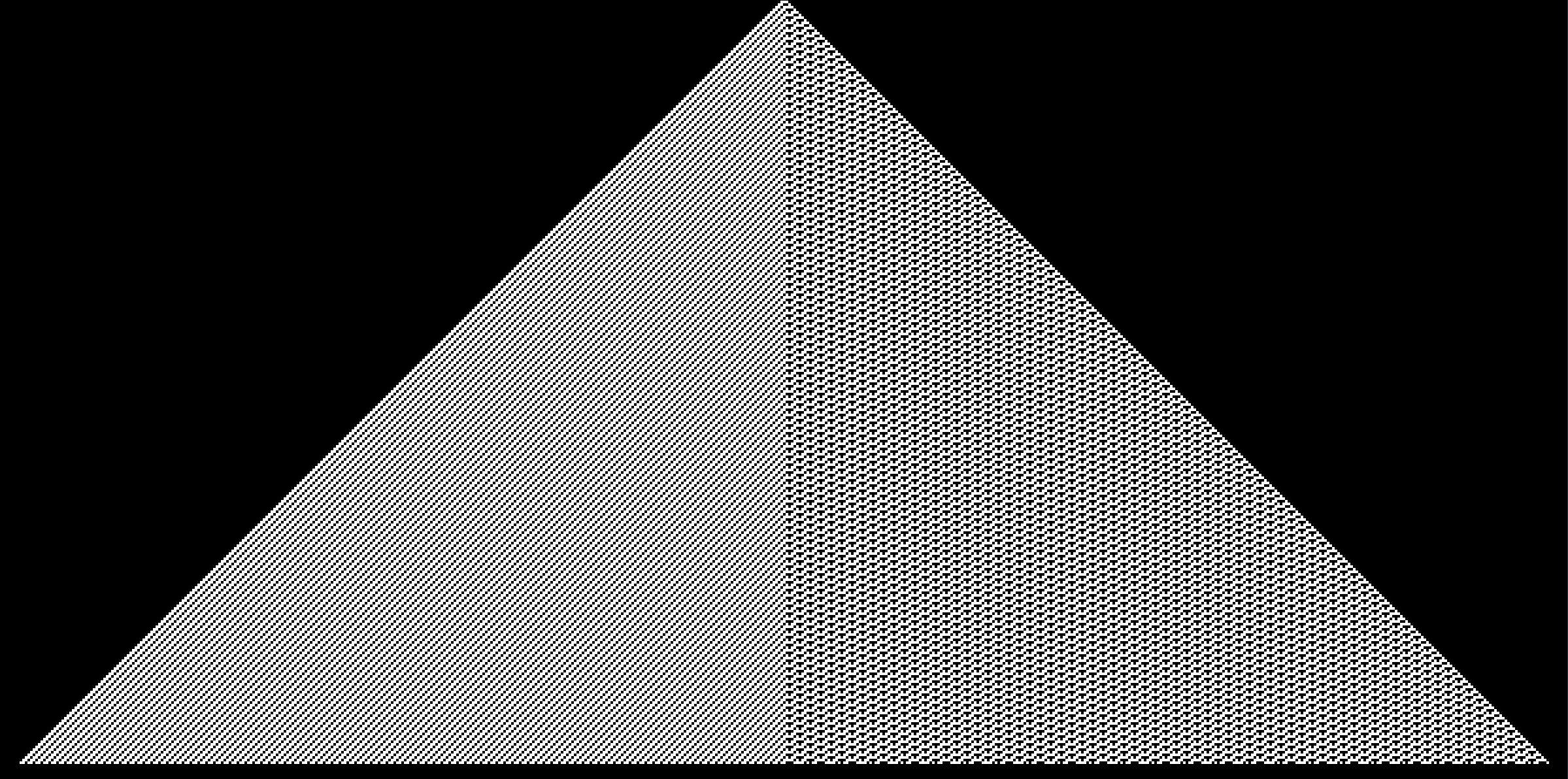
Class I: everything dies after a while
Class I: everything dies after a while
Class III: we are not in class II and so we have something that is 'chaotic', if we measure things like 'spatial' entropy (i.e. the number of bits needed to describe an $N$-bit slice taken at random at time $t$, when $N$ is large, divided by $N$), then it eventually decreases to some constant that is positive
Class III: we are not in class II and so we have something that is 'chaotic', if we measure things like 'spatial' entropy (i.e. the number of bits needed to describe an
N-bit slice taken at random at time
t, when
N is large, divided by
N), then it eventually decreases to some constant that is positive
Class IV: things that don't fit in the above classes, i.e. where the spatial entropy does not always stabilize to some constant (depends on the run, and on the time we run)
Class IV: things that don't fit in the above classes, i.e. where the spatial entropy does not always stabilize to some constant (depends on the run, and on the time we run)
What is interesting in Wolfram's classification
What is interesting in Wolfram's classification
About the Halting Problem (and Decidability)
About the Halting Problem (and Decidability)
Wolfram's Proposed Approach
Wolfram's Proposed Approach
For a rule, just start with random initial configurations... and ask what can we say?
•
For a rule, just start with random initial configurations... and ask what can we say?
Questions about Wolfram's Approach
Questions about Wolfram's Approach
Are we making the conjecture that things cannot be simultaneously chaotic and Turing-complete?
•
Are we making the conjecture that things cannot be simultaneously chaotic and Turing-complete?
Are we making the conjecture that we can discover Turing-complete CA models by sampling things with random initial conditions?
•
Are we making the conjecture that we can discover Turing-complete CA models by sampling things with random initial conditions?
What does exactly periodic mean?
•
What does exactly periodic mean?
The way rule 110 is discovered without pre-engineering, just by ruling out possibilities is very appealing
•
The way rule 110 is discovered without pre-engineering, just by ruling out possibilities is very appealing
What does Turing complete mean?
•
What does Turing complete mean?
What does chaotic mean?
•
What does chaotic mean?
Are we making a statement about what we are _likely to encounter_?
•
Are we making a statement about what we are likely to encounter?
The idea that Turing-completeness can be detected from simple statistical properties is appealing (though clearly wrong in general)
•
The idea that Turing-completeness can be detected from simple statistical properties is appealing (though clearly wrong in general)
Maybe the statement is that the statistics says something about _detecting Turing-completeness_ (positively)
•
Maybe the statement is that the statistics says something about detecting Turing-completeness (positively)
There is a deep question of how much information we put into our description, and what we are supposed to detect from there
•
There is a deep question of how much information we put into our description, and what we are supposed to detect from there
How this question arose (quite) naturally
How this question arose (quite) naturally
After the Game of Life, and a few subsequent works, the research on CAs moved away from self-replication and life in general, and more towards modeling various phenomena appearing in nature (gases, fluids, simple physics, ...)
After the Game of Life, and a few subsequent works, the research on CAs moved away from self-replication and life in general, and more towards modeling various phenomena appearing in nature (gases, fluids, simple physics, ...)
A new direction to the study of CAs was given by Wolfram: study the space of CAs in its entirety, using random CAs and analyze these random CAs using random configurations
A new direction to the study of CAs was given by Wolfram: study the space of CAs in its entirety, using random CAs and analyze these random CAs using random configurations
Some topics for today
Some topics for today
How many simple CAs are there out there?
•
How many simple CAs are there out there?
Show that there are effectively 88 rules modding out the 'obvious' symmetries, and even 32 if we want left-right symmetry evolution for each possible configuration
Show that there are effectively 88 rules modding out the 'obvious' symmetries, and even 32 if we want left-right symmetry evolution for each possible configuration
Class II: we end up 'quickly' with a configuration that is periodic in time, and where if we make a small change on a single cell, it doesn't perturb 'too much' around
Class II: we end up 'quickly' with a configuration that is periodic in time, and where if we make a small change on a single cell, it doesn't perturb 'too much' around
A Bold Conjecture
A Bold Conjecture
Class IV cellular automata are Turing-complete
Class IV cellular automata are Turing-complete
(Implicitly: the other classes are not)
(Implicitly: the other classes are not)
At the time: Von Neumann's CA was clearly Turing-complete and the Game of Life had been recently shown to be Turing-complete
At the time: Von Neumann's CA was clearly Turing-complete and the Game of Life had been recently shown to be Turing-complete
Then he predicts that: you cannot predict anything about a class IV CA without running it
Then he predicts that: you cannot predict anything about a class IV CA without running it
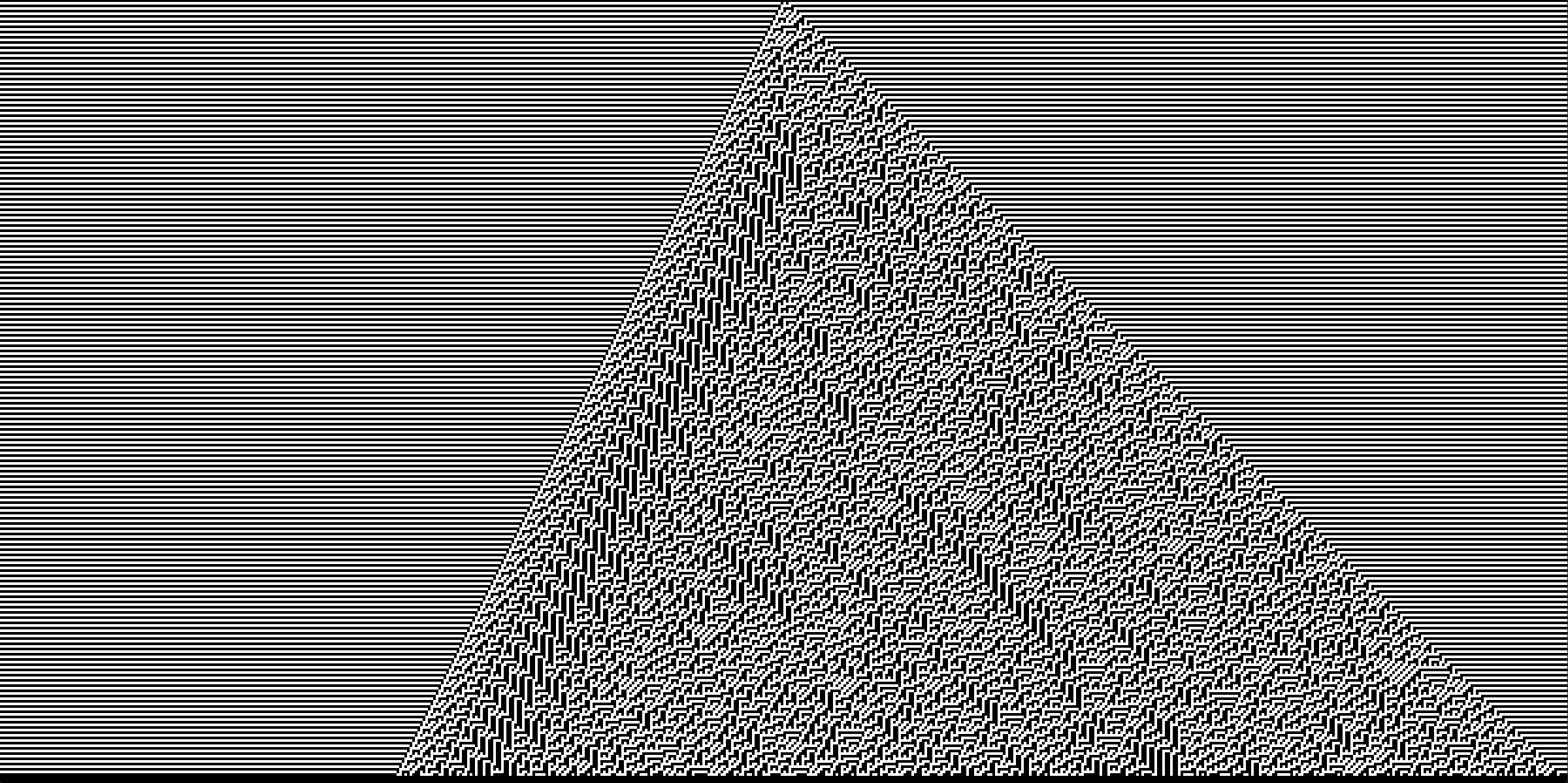
This conjecture is (probably) mostly based on the main example with fluctuating spatial entropy, which is rule 110, where 'glider-like' structures can be observed, and this is reminiscent of Game of Life gliders, which were recently shown to be the key toward showing that the Game of Life is Turing-complete
This conjecture is (probably) mostly based on the main example with fluctuating spatial entropy, which is rule 110, where 'glider-like' structures can be observed, and this is reminiscent of Game of Life gliders, which were recently shown to be the key toward showing that the Game of Life is Turing-complete
This conjecture that rule 110 is Turing-complete was shown by Matthew Cook in 1998
This conjecture that rule 110 is Turing-complete was shown by Matthew Cook in 1998
$110=64+32+8+4+2$, meaning that $110\leadsto 1$,$101\leadsto 1$,$011\leadsto 1$, $010\leadsto1$, $001\leadsto1$, and everything else goes to $0$
110=64+32+8+4+2, meaning that
110⇝1,
101⇝1,
011⇝1,
010⇝1,
001⇝1, and everything else goes to
0 The other rule where one could expect to have Turing-completeness is $54$, but that remains unproven
The other rule where one could expect to have Turing-completeness is
54, but that remains unproven
Proving that the other rules are *not* Turing-complete seems hard, also
Proving that the other rules are not Turing-complete seems hard, also
If we apply this naively to Von Neumann's CA, this would likely fail
▸
If we apply this naively to Von Neumann's CA, this would likely fail
For instance, there are cryptographic primitives that would make arbitrary computations while looking perfectly random on the surface
▸
For instance, there are cryptographic primitives that would make arbitrary computations while looking perfectly random on the surface
Perhaps, but that's not said anywhere
▸
Perhaps, but that's not said anywhere
Somehow still unclear, in particular for rule 54, some things look periodic
▸
Somehow still unclear, in particular for rule 54, some things look periodic
There is an easy 'definition' with spatial entropy, but does it correspond to other notions?
There is an easy 'definition' with spatial entropy, but does it correspond to other notions?
For rule 110, it ended up meaning that you can encode an Turing machine tape state in a very sophisticated manner, then run the rule 110, and then decode (in an even more sophisticated manner) the result
▸
For rule 110, it ended up meaning that you can encode an Turing machine tape state in a very sophisticated manner, then run the rule 110, and then decode (in an even more sophisticated manner) the result
Does it imply we have self-replicators?
•
Does it imply we have self-replicators?
Likely no, but not clear
▸
Likely no, but not clear
The Halting Theorem (by Turing) says that there is no computer program $H$ of finite length that given a program $P$ and an input $X$ returns 'Halts' of 'Infinite Loop' correctly
The Halting Theorem (by Turing) says that there is no computer program
H of finite length that given a program
P and an input
X returns 'Halts' of 'Infinite Loop' correctly
Proof: suppose it exists, and define the program $D$ which takes as input the source of a program $X$, and does
Proof: suppose it exists, and define the program
D which takes as input the source of a program
X, and does
if H(X, X) return 'Halts': do while (True) # infin. loop
else: return 'Cool'
Now look at $D(D)$: if $D(D)$ halts, then it goes into an infinite loop, and if $D(D)$ goes into an infinite loop, then it returns 'Cool', meaning it terminates (so not an infinite loop)
Now look at
D(D): if
D(D) halts, then it goes into an infinite loop, and if
D(D) goes into an infinite loop, then it returns 'Cool', meaning it terminates (so not an infinite loop)
Conclusion: $H$ as a finite-length program cannot exist, otherwise $D$ would exist
Conclusion:
H as a finite-length program cannot exist, otherwise
D would exist
What does 110 mean as a rule?
What does 110 mean as a rule?
.