Reversibility and Arrows of Time

Reversibility and Arrows of Time

In the last lecture, we started discussing cellular automata in general, in particular, we discussed the link between the (lack of) injectivity and the (lack of) surjectivity, with the Moore and Myhill theorems (and the links with the Gardens of Eden)

In the last lecture, we started discussing cellular automata in general, in particular, we discussed the link between the (lack of) injectivity and the (lack of) surjectivity, with the Moore and Myhill theorems (and the links with the Gardens of Eden)

The two cellular automata that we have studied so far (the Von Neumann CA and the Game of Life) are time-irreversible (they are clearly not injective or surjective, and as a result there is no CA that can run their dynamics 'backwards')

The two cellular automata that we have studied so far (the Von Neumann CA and the Game of Life) are time-irreversible (they are clearly not injective or surjective, and as a result there is no CA that can run their dynamics 'backwards')

Von Neumann remarked that he expected that self-reproduction is linked with irreversibility, which intuitively comes from the reason that logical processing is typically non-reversible in time

Von Neumann remarked that he expected that self-reproduction is linked with irreversibility, which intuitively comes from the reason that logical processing is typically non-reversible in time

Even setting computation aside, if we think of a creature growing and making copies of itself in a medium, it feels like to grow (i.e. replicate its own information) it should (in practice) erase some information contained in the medium

Even setting computation aside, if we think of a creature growing and making copies of itself in a medium, it feels like to grow (i.e. replicate its own information) it should (in practice) erase some information contained in the medium

Reproduction and Irreversibility

Reproduction and Irreversibility

Interesting questions about irreversibility

Interesting questions about irreversibility

Where does irreversibility come from when performing computations?

•

Where does irreversibility come from when performing computations?

Can we (artificially) make a CA reversible by adding some additional degrees of freedom?

•

Can we (artificially) make a CA reversible by adding some additional degrees of freedom?

Why do we expect that computational irreversibility says that $P$ is different from $NP$?

•

Why do we expect that computational irreversibility says that $P$ is different from $NP$?

Can we detect that irreversible computations are being performed by a system?

•

Can we detect that irreversible computations are being performed by a system?

Are physical systems that perform irreversible computations somehow alive?

•

Are physical systems that perform irreversible computations somehow alive?

What is the thermodynamical significance of being time-reversible or not?

•

What is the thermodynamical significance of being time-reversible or not?

The origin of irreversibility in computation

The origin of irreversibility in computation

The AND and the OR gates are non-reversible: if we consider a bit, and take the AND of it, with another bit, if that other bit is $0$, we will lose the information on the first bit

The AND and the OR gates are non-reversible: if we consider a bit, and take the AND of it, with another bit, if that other bit is $0$, we will lose the information on the first bit

The thermodynamics significance of this

The thermodynamics significance of this

(Note that in quantum computing, computations are reversible, until we collapse the state)

(Note that in quantum computing, computations are reversible, until we collapse the state)

If we view the computation as a thermodynamics process, it is clearly an irreversible one, and so some entropy should have been created on the way

If we view the computation as a thermodynamics process, it is clearly an irreversible one, and so some entropy should have been created on the way

This is the so-called Landauer's principle, which postulates that the erasure of one bit of information amounted to a dissipation of energy at least equal to $k_BT\ln2$, and this sets a lower bound on the energy consumption (dissipation) of _any_ computation

This is the so-called Landauer's principle, which postulates that the erasure of one bit of information amounted to a dissipation of energy at least equal to $k_BT\ln2$, and this sets a lower bound on the energy consumption (dissipation) of any computation

This was also seen to be in connection with the Maxwell Demon's paradox: the demon needs to perform computations and hence must create entropy

This was also seen to be in connection with the Maxwell Demon's paradox: the demon needs to perform computations and hence must create entropy

This idea stimulated the research is 'reversible computing' where one would try to make computations as reversible possible, by doing some 'book-keeping' (if the 'lost' bits of information go somewhere, then they are not 'lost' and would not dissipate energy)

This idea stimulated the research is 'reversible computing' where one would try to make computations as reversible possible, by doing some 'book-keeping' (if the 'lost' bits of information go somewhere, then they are not 'lost' and would not dissipate energy)

This also led to Toffoli proposing a reversible cellular automaton construction

This also led to Toffoli proposing a reversible cellular automaton construction

Toffoli's Result

Toffoli's Result

Any cellular automaton in dimension $d$ (i.e. on $\mathbb Z^d$) can be simulated in 'real time' as a 'slice' of a reversible cellular automaton in dimension $d+1$ (i.e. on $\mathbb Z^{d+1}$)

Any cellular automaton in dimension $d$ (i.e. on $\mathbb Z^d$) can be simulated in 'real time' as a 'slice' of a reversible cellular automaton in dimension $d+1$ (i.e. on $\mathbb Z^{d+1}$)

Exercise: this is not true if we don't add the extra dimension

Exercise: this is not true if we don't add the extra dimension

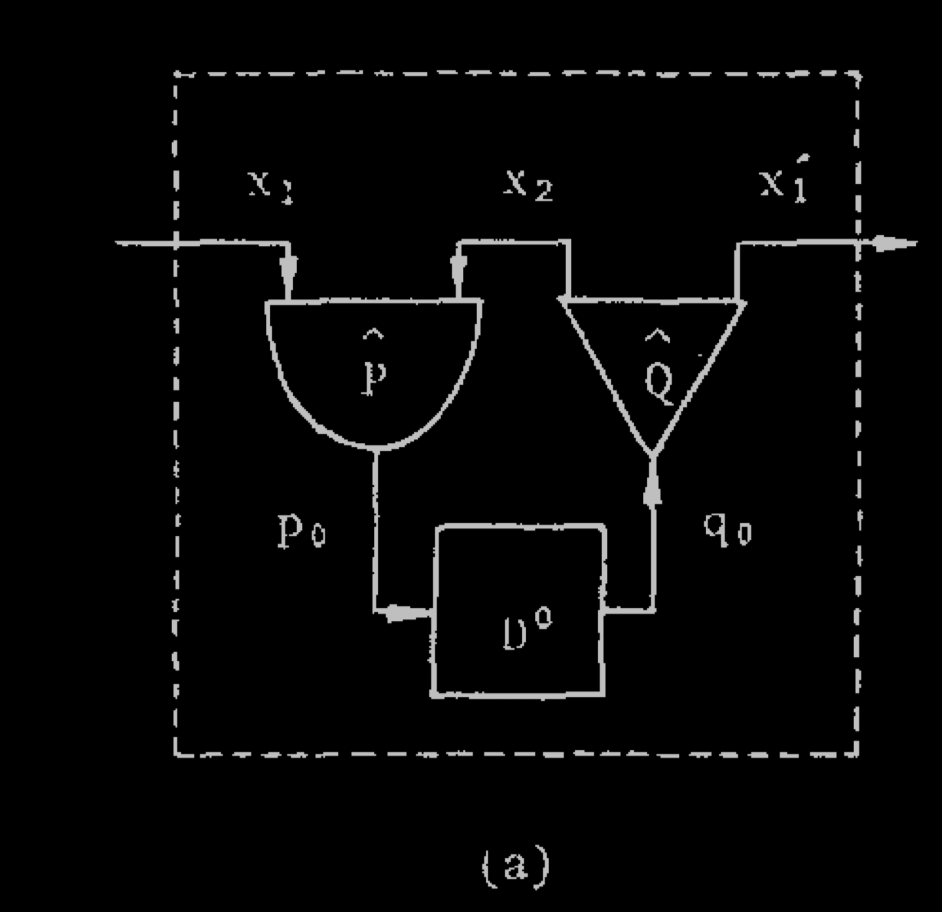
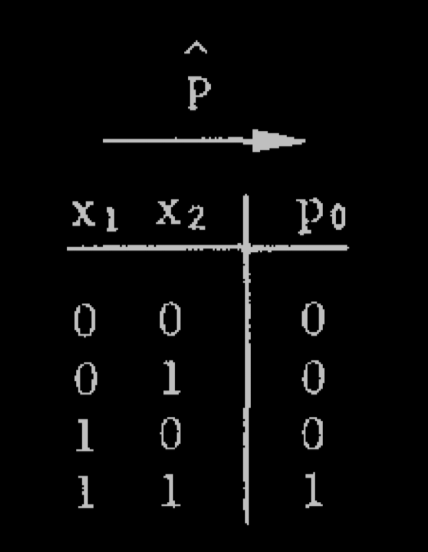
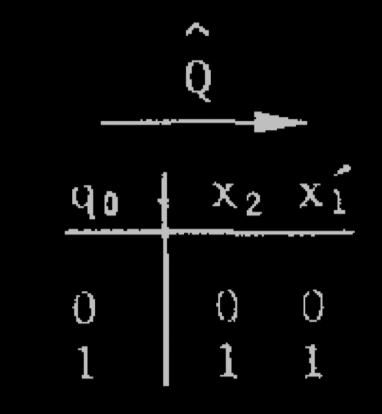
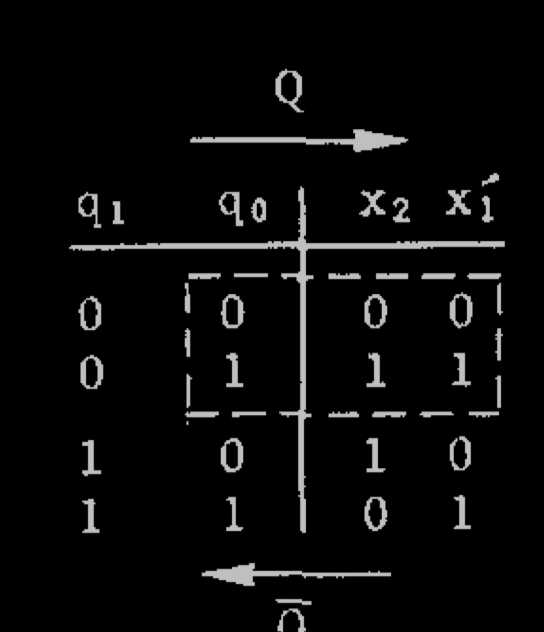
Let us describe the construction of Toffoli for a specific one-dimensional cellular automaton which is just a binary automaton, where each state is updated by taking the and of itself with its left neighbor (as was done in his original paper, from which we borrow the figures)

Let us describe the construction of Toffoli for a specific one-dimensional cellular automaton which is just a binary automaton, where each state is updated by taking the and of itself with its left neighbor (as was done in his original paper, from which we borrow the figures)

Basic forward circuit: $P$ is an AND gate, $Q$ is a disjunction (split the info), $D$ is a delay

Basic forward circuit: $P$ is an AND gate, $Q$ is a disjunction (split the info), $D$ is a delay

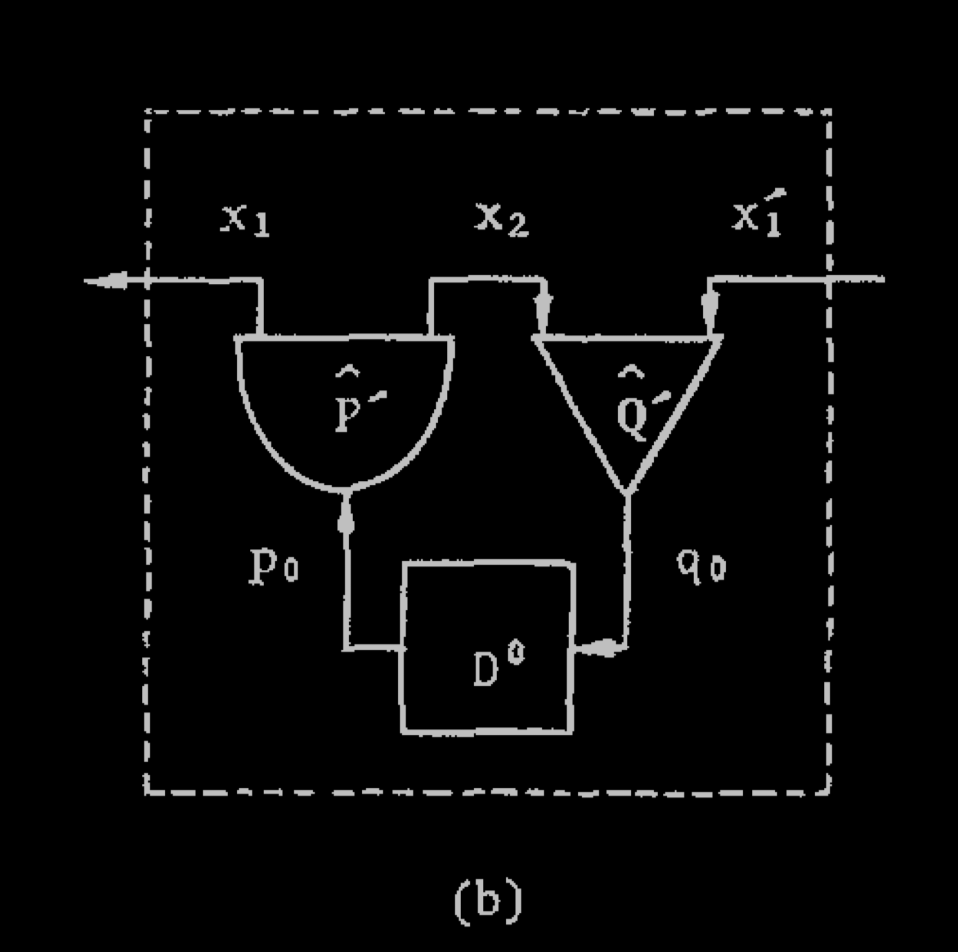
Naive attempt to reverse the forward circuit

Naive attempt to reverse the forward circuit

$P$ truth table

$P$ truth table

$Q$ truth table

$Q$ truth table

$\hat P$ truth table

$\hat P$ truth table

$\hat Q$ truth table

$\hat Q$ truth table

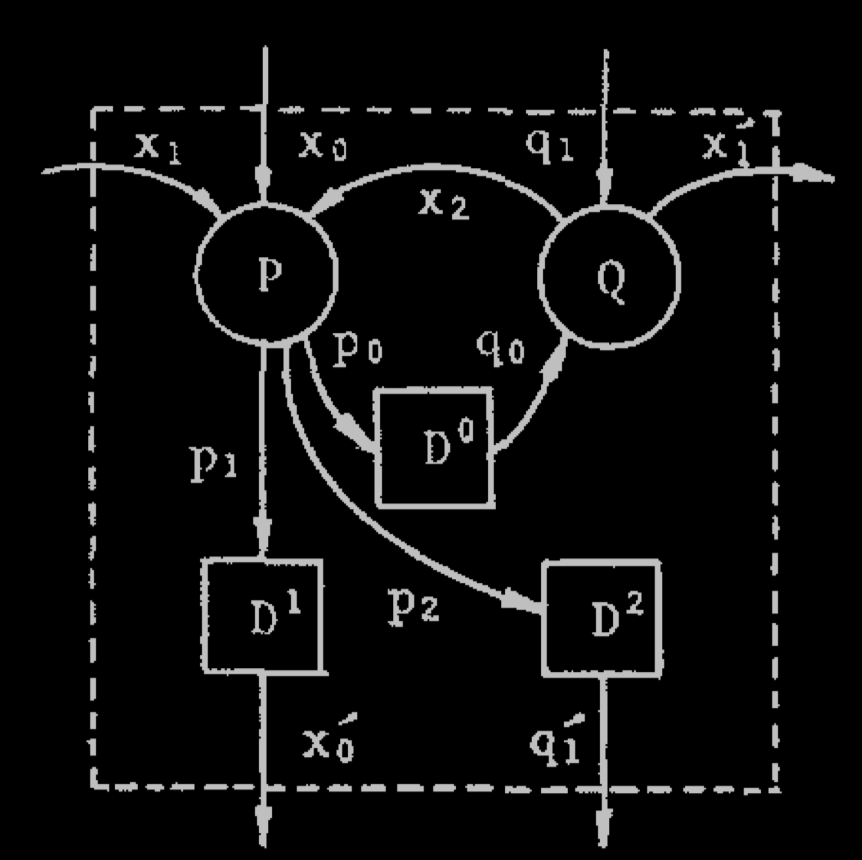
Extended forward circuit

Extended forward circuit

Extended backward circuit

Extended backward circuit

Schematization of embedding in $2$ dimensions

Schematization of embedding in $2$ dimensions

What is nice with this construction

What is nice with this construction

It does not really prove that Von Neumann was wrong, that self-replication cannot happen in a medium without reversibility

It does not really prove that Von Neumann was wrong, that self-replication cannot happen in a medium without reversibility

But it is still nice to have a book-keeping mechanism where we really see the entropy production

But it is still nice to have a book-keeping mechanism where we really see the entropy production

Remark: anyway, it is well known that if we keep track of absolutely all the degrees of freedom of a system, we are reversible, and we don't create entropy

Remark: anyway, it is well known that if we keep track of absolutely all the degrees of freedom of a system, we are reversible, and we don't create entropy

Toffoli's construction does a bit the reverse of the usual thing: expand degrees of freedom artificially to be reversible

Toffoli's construction does a bit the reverse of the usual thing: expand degrees of freedom artificially to be reversible

Why $P$ is different from $NP$?

Why $P$ is different from $NP$?

Take an example of a classical problem (not $NP$ complete, but in some ways nicer): if we take two large prime numbers $p,q$ with $p < q$, we can easily compute their product $pq$, but then somehow it is hard to recover them from their product, though technically the information is the same

Take an example of a classical problem (not $NP$ complete, but in some ways nicer): if we take two large prime numbers $p,q$ with $p < q$, we can easily compute their product $pq$, but then somehow it is hard to recover them from their product, though technically the information is the same

Something that we would like to try is to reverse the multiplication, and the reason we fail is because there are some bits of information lost in the process

Something that we would like to try is to reverse the multiplication, and the reason we fail is because there are some bits of information lost in the process

If we try to go back for each of the operations that led to the product, we will see that there will be many times where there were several possible 'previous steps', and this leads to a branching tree of possibilities

If we try to go back for each of the operations that led to the product, we will see that there will be many times where there were several possible 'previous steps', and this leads to a branching tree of possibilities

If we apply this line of reasoning for problems in $NP$, i.e. problems where there is a polynomial-sized circuit (hence polynomial depth) checking the solution, we could do the same: try to backtrack from the 'solution checks correct' to the solution itself, and find ourselves with branchings due to the irreversibility of the circuit operations

If we apply this line of reasoning for problems in $NP$, i.e. problems where there is a polynomial-sized circuit (hence polynomial depth) checking the solution, we could do the same: try to backtrack from the 'solution checks correct' to the solution itself, and find ourselves with branchings due to the irreversibility of the circuit operations

(Ideas suggested to me by Ron Maimon)

(Ideas suggested to me by Ron Maimon)

This suggests why the 'worst' $NP$ problems should take exponential time to solve: if the circuit has at least linear depth, and if at every depth level, we lose at least one bit of information, then 'generically' (unless we are lucky with the problem instance) we have an exponential branching to resolve to go backwards (there does not seem to be a useful strategy for backtracking)

This suggests why the 'worst' $NP$ problems should take exponential time to solve: if the circuit has at least linear depth, and if at every depth level, we lose at least one bit of information, then 'generically' (unless we are lucky with the problem instance) we have an exponential branching to resolve to go backwards (there does not seem to be a useful strategy for backtracking)

So, this suggests that (in the worst case, and perhaps also in the 'average random case') we should resolve an exponential number of branchings, thus requiring an exponential number of steps

So, this suggests that (in the worst case, and perhaps also in the 'average random case') we should resolve an exponential number of branchings, thus requiring an exponential number of steps

Of course, the above argument has not been made rigorous (otherwise that would be the solution to the $P$ vs $NP$ problem), but it suggests a clear interesting link between irreversibility and computatability

Of course, the above argument has not been made rigorous (otherwise that would be the solution to the $P$ vs $NP$ problem), but it suggests a clear interesting link between irreversibility and computatability

Recognizing Computations with LLMs

Recognizing Computations with LLMs

An interesting related question that the above suggests is:

An interesting related question that the above suggests is:

Can we _recognize_ if a dynamical system is performing non-trivial computations?

•

Can we recognize if a dynamical system is performing non-trivial computations?

... and this turns out to be related to a question we investigated using LLMs recently!

... and this turns out to be related to a question we investigated using LLMs recently!

Arrows of Time and Large Language Models

Arrows of Time and Large Language Models

(Work with Vassilis Papadopoulos and Jérémie Wenger)

(Work with Vassilis Papadopoulos and Jérémie Wenger)

Models like GPT famously predict the _next symbol_ in a dataset, given the previous one

Models like GPT famously predict the next symbol in a dataset, given the previous one

This corresponds to a factorization of probabilities $\mathbb P\{X_1=x_1,\ldots,X_n=x_n\}$

This corresponds to a factorization of probabilities $\mathbb P\{X_1=x_1,\ldots,X_n=x_n\}$

What if we do things backwards? $\mathbb P\{X_{k-1}=x_{k-1}|X_k=x_k,\ldots,X_n=x_n\}$

What if we do things backwards? $\mathbb P\{X_{k-1}=x_{k-1}|X_k=x_k,\ldots,X_n=x_n\}$

Theoretically, we are just factorizing the same probability measure in different ways, so it would be reasonable to expect that, given a dataset, we end up modeling the same measure

•

Theoretically, we are just factorizing the same probability measure in different ways, so it would be reasonable to expect that, given a dataset, we end up modeling the same measure

$\mathbb P\{X_{k+1}=x_{k+1}|X_1=x_1,\ldots,X_k=x_k\}$

•

This corresponds to a different factorization of $\mathbb P\{X_1=x_1,\ldots,X_n=x_n\}$

•

This corresponds to a different factorization of $\mathbb P\{X_1=x_1,\ldots,X_n=x_n\}$

On natural language datasets, however, we see that there is a universal difference: the 'forward' modeling direction does systematically better than then 'backward direction'

•

On natural language datasets, however, we see that there is a universal difference: the 'forward' modeling direction does systematically better than then 'backward direction'

Trying to find theoretical reasons for this, we first ended up with the example of the product of two numbers: if we try to predict $pq$ from $p$ and $q$, then it is substantially easier than if we try to predict $p$ and $q$ from $pq$, though they contain the same information

•

Trying to find theoretical reasons for this, we first ended up with the example of the product of two numbers: if we try to predict $pq$ from $p$ and $q$, then it is substantially easier than if we try to predict $p$ and $q$ from $pq$, though they contain the same information

Then we explored a very simple model of language computation, where a sparse invertible binary matrix is systematically applied to a (random assignment) to a register, hence leading us to learn the matrix

•

Then we explored a very simple model of language computation, where a sparse invertible binary matrix is systematically applied to a (random assignment) to a register, hence leading us to learn the matrix

To go backward in time is actually harder, because we need to learn the inverse of the (sparse) matrix, which is typically somehow less sparse

•

To go backward in time is actually harder, because we need to learn the inverse of the (sparse) matrix, which is typically somehow less sparse

Though this is a toy model, we think that this capture something about computation done in e.g. a living system: the sparsity is related to the fact that the circuit is constrained by the space and energy available; by default, even if we don't lose information per se, the backward computation will typically be less easy

•

Though this is a toy model, we think that this capture something about computation done in e.g. a living system: the sparsity is related to the fact that the circuit is constrained by the space and energy available; by default, even if we don't lose information per se, the backward computation will typically be less easy

The reason for this is not a priori a 'loss' of information as in thermodynamics, because we are trying to process the _same information_, just in two different directions; it is the way the information is processed

•

The reason for this is not a priori a 'loss' of information as in thermodynamics, because we are trying to process the same information, just in two different directions; it is the way the information is processed

Somehow, it seems reasonable at this point to postulate that this is a sign of life

•

Somehow, it seems reasonable at this point to postulate that this is a sign of life

In the case of language, we modeled this with Alice and Bob trying to communicate, and Alice only sending messages to Bob if they are 'easy to process' (which we understand as 'forward-sparse'), and seeing that the backward-learning

•

In the case of language, we modeled this with Alice and Bob trying to communicate, and Alice only sending messages to Bob if they are 'easy to process' (which we understand as 'forward-sparse'), and seeing that the backward-learning

How this relates to the Von Neumann's idea

How this relates to the Von Neumann's idea

Von Neumann suggested that irreversibility, in the form of entropy creation, is a necessary condition for life... we believe that this is true, but there is a lot of things in the universe that creates entropy and that is not life, so this is by no means a sufficient condition

Von Neumann suggested that irreversibility, in the form of entropy creation, is a necessary condition for life... we believe that this is true, but there is a lot of things in the universe that creates entropy and that is not life, so this is by no means a sufficient condition

Our work on arrows of time for large language models seems to suggest that a more subtle version of irreversibility, not directly about entropy creation, related somehow to sparsity asymmetry, is the sign that something is computing, and should be interpreted as a sign of life

Our work on arrows of time for large language models seems to suggest that a more subtle version of irreversibility, not directly about entropy creation, related somehow to sparsity asymmetry, is the sign that something is computing, and should be interpreted as a sign of life